# Machine Learning
**Repository Path**: lhscau/machine-learning
## Basic Information
- **Project Name**: Machine Learning
- **Description**: No description available
- **Primary Language**: Unknown
- **License**: Not specified
- **Default Branch**: master
- **Homepage**: None
- **GVP Project**: No
## Statistics
- **Stars**: 0
- **Forks**: 8
- **Created**: 2022-04-26
- **Last Updated**: 2022-05-24
## Categories & Tags
**Categories**: Uncategorized
**Tags**: None
## README
# 机器学习
文章链接
~~~bash
https://gitee.com/fakerlove/machine-learning
~~~
#
# 1. 概念
## 1.1 简介
### 1.1.1 人工智能
人工智能之父-图灵
人工智能:机器模拟人的意识和思维
**人工智能是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门技术科学。**“人工智能”是“一门技术科学”,它研究与开发的对象是“理论、技术及应用系统”,研究的目的是为了“模拟、延伸和扩展人的智能”。
人工智能的研究领域也在不断扩大,图二展示了人工智能研究的各个分支,包括专家系统、机器学习、进化计算、模糊逻辑、计算机视觉、自然语言处理、推荐系统等。
#### 1) 发展方向
人工智能大致分三个方向
* 计算机视觉
人脸识别
图像形成
* 自然语言处理(NLP)
文本挖掘和分类
机器翻译
语音识别
* 机器人
#### 2) 三要素
* 数据
* 算法
* 计算力
### 1.1.2 机器学习
机器学习:一种实现人工智能的方法
机器学习(Machine Learning)是指用某些算法指导计算机利用已知数据得出适当的模型,并利用此模型对新的情境给出判断的过程。
机器学习的思想并不复杂,它仅仅是对人类生活中学习过程的一个模拟。而在这整个过程中,最关键的是数据。
任何通过数据训练的学习算法的相关研究都属于机器学习,包括很多已经发展多年的技术,比如线性回归(Linear Regression)、K均值(K-means,基于原型的目标函数聚类方法)、决策树(Decision Trees,运用概率分析的一种图解法)、随机森林(Random Forest,运用概率分析的一种图解法)、PCA(Principal Component Analysis,主成分分析)、SVM(Support Vector Machine,支持向量机)以及ANN(Artificial Neural Networks,人工神经网络)。

### 1.1.3 深度学习
深度学习(Deep Learning)的概念源于人工神经网络的研究。含多隐层的多层感知器就是一种深度学习结构。深度学习通过组合低层特征形成更加抽象的高层表示属性类别或特征,以发现数据的分布式特征表示。
深度学习是机器学习研究中的一个新的领域,其动机在于建立、模拟人脑进行分析学习的神经网络,它模仿人脑的机制来解释数据,例如图像,声音和文本。
深度学习:一种实现机器学习的技术,深度学习,作为目前最热的机器学习方法,但并不意味着是机器学习的终点。
## 1.2 书本网站推荐

网址
~~~bash
https://cs231n.Stanford.edu
~~~
第二个网址-吴恩达的学习网站
~~~bash
https://www.coursera.org/learn/machine-learning
~~~
机器学习平台
~~~python
https://studio.azureml.net/
~~~
## 1.3 三者关系
在**人工智能**的大陆上,有很多家族,其中最大的一个家族就是**机器学习**,其中现任族长叫做**深度学习**,手上有个特殊的绝技**神经网络**。现在有个不安分的弟子想篡位叫做**强化学习**
> 严格意义上说,人工智能和机器学习没有直接关系,只不过目前机器学习的方法被大量的应用于解决人工智能的问题而已。目前机器学习是人工智能的一种实现方式,也是最重要的实现方式。
>
> 早期的机器学习实际上是属于统计学,而非计算机科学的;而二十世纪九十年代之前的经典人工智能跟机器学习也没有关系。所以今天的AI和ML有很大的重叠,但并没有严格的从属关系。
>
> 不过如果仅就计算机系内部来说,ML是属于AI的。AI今天已经变成了一个很泛泛的学科了。

如果把人工智能与机器学习当成两个学科来看,三者关系如下图所示:
向左转|向右转

如果把深度学习当成人工智能的一个子学科来看,三者关系如下图所示
向左转|向右转

## 1.4 十大算法
### 1.4.1 监督学习
supervised learning;
有监督学习,就是有正确的答案的训练数据
输入数据即由输入特征和目标值所组成,
#### 1) 决策树
(Decision Trees)
决策树是一个决策支持工具,它使用树形图或者决策模型以及可能性序列,包括偶然事件的结果、资源成本和效用。
#### 2) 朴素贝叶斯分类
(Naive Bayesian classification)
朴素贝叶斯分类器是一类简单的概率分类器,它基于贝叶斯定理和特征间的强大的(朴素的)独立假设。
一些应用例子:
- 判断垃圾邮件
- 对新闻的类别进行分类,比如科技、政治、运动
- 判断文本表达的感情是积极的还是消极的
- 人脸识别
#### 3) 最小二乘法
(Ordinary Least Squares Regression)
如果你懂统计学的话,你可能以前听说过线性回归。最小二乘法是一种计算线性回归的方法。你可以将线性回归看做通过一组点来拟合一条直线。实现这个有很多种方法,“最小二乘法”就像这样:你可以画一条直线,然后对于每一个数据点,计算每个点到直线的垂直距离,然后把它们加起来,那么最后得到的拟合直线就是距离和尽可能小的直线。
#### 4) 逻辑回归
(Logistic Regression)
逻辑回归是一个强大的统计学方法,它可以用一个或多个解释变量来表示一个二项式结果。它通过使用逻辑函数来估计概率,从而衡量类别依赖变量和一个或多个独立变量之间的关系,后者服从累计逻辑分布。
#### 5) 支持向量机
(Support Vector Machine,SVM)
SVM是二进制分类算法。给定N维坐标下两种类型的点,SVM生成(N-1)维的超平面来将这些点分成两组。假设你在平面上有两种类型的可以线性分离的点,SVM将找到一条直线,将这些点分成两种类型,并且这条直线尽可能远离所有这些点。
#### 6) 集成方法
(Ensemble methods)
集成方法是学习算法,它通过构建一组分类器,然后通过它们的预测结果进行加权投票来对新的数据点进行分类。原始的集成方法是贝叶斯平均,但是最近的算法包括纠错输出编码、Bagging和Boosting。
##### Adaboost
#### 7) K近邻
**KNN(K Nearest Neighbor)**
K表示K个邻居,不表示距离,因为需要求所有邻居的距离,所以效率低下。
优点:可以用来填充缺失值,可以处理非线性问题
调优方法:K值的选择,k值太小,容易过拟合
应用:样本数少,特征个数较少,kNN更适合处理一些分类规则相对复杂的问题,在推荐系统大量使用
KNN算法和贝叶斯算法有某种神秘的联系,用贝叶斯算法估算KNN的误差。
### 1.4.2 非监督学习
unsupervised learning;
#### 1) 聚类算法
(Clustering Algorithms)
聚类是将一系列对象分组的任务,目标是使相同组(集群)中的对象之间比其他组的对象更相似。
没有正确答案的训练数据,怎么样都是对的
每一种聚类算法都不相同,下面是一些例子:
- 基于质心的算法
- 基于连接的算法
- 基于密度的算法
- 概率
- 降维
- 神经网络/深度学习
##### K-means K均值
#### 2) 主成分分析
(Principal Component Analysis,PCA)
PCA是一个统计学过程,它通过使用正交变换将一组可能存在相关性的变量的观测值转换为一组线性不相关的变量的值,转换后的变量就是所谓的主分量。
#### 3) 奇异值分解
(Singular Value Decomposition,SVD)
在线性代数中,SVD是复杂矩阵的因式分解。对于给定的m * n矩阵M,存在分解使得M=UΣV,其中U和V是酉矩阵,Σ是对角矩阵。
#### 4) 独立成分分析
(Independent Component Analysis,ICA)
ICA是一种统计技术,主要用于揭示随机变量、测量值或信号集中的隐藏因素。ICA对观测到的多变量数据定义了一个生成模型,这通常是作为样本的一个大的数据库。在模型中,假设数据变量由一些未知的潜在变量线性混合,混合方式也是未知的。潜在变量被假定为非高斯分布并且相互独立,它们被称为观测数据的独立分量。
### 1.4.3 半监督学习
semi-supervised learning
### 1.4.4 强化学习
reinforcement learning;
四要素:agent,action,environemnt,reward
### 1.4.5 遗传算法
genetic algorithm.
## 1.5 基本术语
机器学习的工作流程
* 获取数据
* 数据基本处理
* 特征工程
* 机器学习,模型训练
* 模型评估
就是从数据中自动分析获取数据模型,并利用模型对未知的数据进行训练
* 数据集-100个西瓜
一组记录的集合
* 样本-1个西瓜
数据集中的一条记录
* 特征(属性)-颜色,大小
反映时间或对象在某方面的表现或性质的事项
* 特征向量
以颜色为x轴,大小为y轴,敲声为z轴,每个西瓜都有自己的坐标位置,每个坐标位置对应的坐标向量叫做特征向量
* 学习
从数据中学得模型的过程称为学习或者训练
* 训练数据
训练过程中使用的数据称为训练数据
* 训练样本
数据的每个样本叫做训练样本
* 特征工程
特征工程是使用专业背景知识和技巧处理数据,使用特征能在机器学习算法上发挥更好的作用的过程
说白了就是如何把图像视屏等数据变成机器识别是过程
## 1.6 假设空间
科学的推理手段
* 归纳
特殊到一般
+ 狭义
从训练数据中得到概念
布尔概念;是或者不是
+ 广义
从样本中学习
* 演绎
一般到特殊
## 1.7 归纳偏好
同一个数据集训练出了不同 的模型,应该如何选择模型
一般会使用**奥卡姆剃刀原则**
若有多个假设与观察一致,则选择最简单的哪一个
## 1.8 模型评估
如何评估一个模型到底好还是不好。这个时候就需要我们的模型评估。
用哪些判定的标准来说明一个模型的好坏
一个模型好坏判决的标准1. P-R曲线 2.ROC曲线
### 1.8.1 经验误差与过拟合
* 错误率
通常把分类错误的样本数占样本总数的比例叫做错误率
在m个样本中有a个样本分类错误,错误率E=a/m
* 欠拟合
机器学习到的特征太少,导致区分不太标准,不能准确识别天鹅

* 过拟合
当学习器把训练样本学的太好的时候,很可能已经把训练样本的自身的一些特点当做了所有潜在样本都会具有的一般性质,会导致泛化能力的下降,这种现象叫做过拟合

机器由于学习的特征过多,导致是天鹅的在实际的验证过程中错误。
* 泛化能力
即模型对没有见过的数据的预测能力
* 泛化误差
机器学习在训练集上的误差叫做训练误差或者经验误差,在新的样本上的误差叫做泛化误差
### 1.8.2 评估法
是使用测试集来对学习器对新样本的判断能力。
为啥不直接使用数据集,而是把数据集分成训练集和测试集????
因为模型是用训练集训练的,再用训练集测试一点用处没有,相当于把做过的试卷再做一遍
#### 1) 留出法-测试集
> 直接将数据集D一份为2,一个为训练集S,一份为测试集T,$D=S\cup T$
>
> 使用S训练出模型,然后使用T评估其误差
数据怎么取
直接三七分,前面是70% 为训练集,后面的30% 为测试集
或者随机取抽取一部分数据
#### 2) 交叉验证法-测试集
> 例如一共有10分数据集,
>
> 第一次把$D_{10}$作为测试集,剩下的部分全部作为训练集
>
> 第二次把$D_{9}$作为测试集,剩下的部分全部作为训练集
>
> 依次类推,最后一次把$D_{1}$作为测试集,剩下的部分全部作为训练集.
>
> 一共得出10次结果,这样把结果求个平均值
>
> 
缺点:当数据量较大时,对算力要求较高
#### 3) 自助法-测试集
> 首先了解一个数学极限
>
> $lim_{m\to \infty}(1-\frac{1}{m})^m=\frac{1}{e}=0.368$
>
> 怎么用呢,就是我们随机抽样m份的数据集,记录下数据,放回原样,然后再次取m 分数据,依次类推。重复如此操作m次后,就如同极限一样。取一次m的几率为$1-\frac{1}{m}$的机会,这样子去m次就有36.8%的样本未出现在数据集中,则把36.8%的样本集作为测试集,剩下的样本作为训练集
缺点:改变初始数据集的分布,会引入误差
#### 4) 调参-验证集
> 调参
>
> * 大多数学习算法都需要设定自行设定参数,参数的不同,学习得出的模型性能往往天差地别
>
> 对参数的选择往往是区间内取值,比如有三个参数,每个参数有5种选择,那么测试/训练集就有125个模型需要查看
>
> * 验证集
>
> 是模型评估与选择中用于评估册数的数据集,基于验证集上的性能进行模型的选择和调参。
流程一般如下:
训练集训练,验证集上看结果,进行调参,
再在验证集上看结果,
最后在测试集上看结果
### 1.8.3 性能度量
#### 1) 均方误差
$E(f;D)=\frac{1}{m}\sum_{i=1}^m(f(x_i)-y_i)^2$
如果数据分布D和概率密度函数p(.),均方误差无额
$E(f;D)=\int_{x\sim D}(f(x)-y)^2p(x)dx$
#### 2) 错误率
$E(f;D)=\frac{1}{m}\sum_{i=1}^m\prod (f(x_i)\ne y_i) $
小双杠是统计,满足括号里条件的元素的个数的意思
这个表达式表达的意思为$\frac{统计出来的错误的个数}{总数m}$
E 表示的是error,不是期望
#### 3) 精度
$acc(f;D)=\frac{1}{m}\sum_{i=1}^m\prod (f(x_i)\ y_i)=1-E(f;D)$
就是正确的比率
错误率和精度的优点是:**它们不仅仅适用于二分类问题,也同样适用于多分类问题。**
但是单单看错误率和精度两个指标无法很好的对模型进行合适的评估。一方面,现在不少的模型最终都是预测一个类别的概率值,为了计算错误率和精度,得设定一个阈值,以便确定预测的正例和反例。这样相当于引入了一个新的超参数,会增加复杂性和不确定行。
#### 4) 查准率,查全率和F1
##### 一个二分法
对于二分类问题,样本点的实际类别和预测的类别两辆组合,会产生4种情况:
| 真实情况 | 正例 | 反例 |
| -------- | ---------------------------------- | ---------------------------------- |
| T | TP(原本是正确,也预测成正确) | FN(原本是正确的,但是预测成错误的) |
| 错误的F | FP(原本是错误的,但是预测成正确的) | TN(原本是错误的,预测也是错的) |
也就是说只有TP和TN 是成功的预测的结果,FP,FN是预测错误的
**查准率**
$P=\frac{TP}{TP+FP}$
**查全率**
$R=\frac{TP}{TP+FN}$
在举个例子
抓汉奸的例子吧
| | 真实结果 | 预测结果 | |
| ---- | -------- | ----------- | ------------ |
| 好人 | 不杀 | 好人-不杀 | TP |
| 好人 | 不杀 | 汉奸-杀掉了 | FN(误杀了) |
| 汉奸 | 杀掉 | 好人-不杀 | FP(伪装成功) |
| 汉奸 | 杀掉 | 汉奸-该杀 | TN(成功歼敌) |
* 查准率
说白了,就是查出来的好人中有多少是真正的好人
用西瓜说的话,我挑的瓜有多少比率是好瓜
1-查准率=就是汉奸率是多少
* 查全率
说白了,就是真正的好人,有多少被查出来了。
用西瓜说,就是有多少的好瓜被我挑出来了
1-查全率=说有多少人好人被误杀
对于上面是P和R ,一般会综合考虑P和R,有三种方法进行最优阈值的确定
**方法二F1**
**定义两者的调和平均值为F1**。表示如下:
$\frac{1}{F1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R})$
$F1=\frac{2\times P\times R}{P+R}=\frac{2\times TP}{样本总数+TP-TN}$
调和平均相比较于算数平均,
方法三$F_{\beta}$
如果更加重视较小值。也可以给P和R加上权重,表示如下:
$\frac{1}{F_{\beta}}=\frac{1}{1+\beta^2}(\frac{1}{P}+\frac{\beta ^2}{R})$
更加重视准确率,就意味着“宁缺毋滥”,适用于对精度要求高的场景,如商品推荐。
##### n个二分法
当出现很多个二分类时,最直接的做法是分别计算出每个二分类的查准率和查全率,在计算平均值
得到$TP,FP,TN,FN的平均值\overline{TP},\overline{FP},\overline{TN},\overline{FN}$,在基于这些平均值计算出微查准率和微查全率
#### 6) P-R曲线
一个训练集多种模型如何进行抉择????
将样本按照按照预测为正例的概率值从大到小进行排序,从第一个开始,逐个将当前样本点的预测值设置为阈值,有了阈值之后,即可得出混淆矩阵各项的数值,然后计算出P和R,以R为横坐标,P为纵坐标,绘制于图中,即可得出P-R曲线,示意图如下。

当一个模型a的P-R曲线完全包住另一个模型b的P-R曲线时,即可认为a优于b。
其他情况下,可以使用平衡点,也即F1值,或者曲线下的面积来评估模型的好坏。
#### 7) ROC曲线和AUC
同样使用分类结果的混淆矩阵
| 真实情况 | 正例 | 反例 |
| -------- | ---------------------------------- | ---------------------------------- |
| 正确的T | TP(原本是正确,也预测成正确) | FN(原本是正确的,但是预测成错误的) |
| 错误的F | FP(原本是错误的,但是预测成正确的) | TN(原本是错误的,预测也是错的) |
$TPR=\frac{TP}{TP+FN}$
$FPR=\frac{FP}{TN+FP}$
以FPR为横坐标,TPR为纵坐标,即可绘制出ROC(Receiver Operating Characteristic)曲线
用于评估模型的好坏,面积的计算可以通过梯形去插值计算,公式和示意图如下:
$AUC=\frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1}-x_i)(y_{i+1}+y_i)$
通俗点,AUC 就是阴影部分的面积,用来评估样本不平衡的情况
和P-R曲线一样,当一个模型a的ROC曲线完全包住另一个模型b的ROC曲线时,即可认为a优于b。
##### ROC 怎么绘制
链接
~~~python
https://www.zhihu.com/question/63492375/answer/1313378782
~~~
假设有10个方块,其中有7个好方块(白色),3个坏方块(黑色),编号为0-10

**模型**
我们已经训练好了一个分类模型M ,我们将方块输入这个模型,这个模型可以给每一个方块打分。这里我们假设打分范围是0-1分,分数越大,则模型认为该方块为**好方块**的几率越大。
**将10个方块输入模型**
我们将10个方块输入模型,得到每个方块的打分。

我们按照分数由高到低给方块排序。如下图:

**设置第一个阈值**
当我们设置阈值为0.90时,模型M 打分$\ge$0.90则为好方块, $\le$0.90则为坏方块。
在我们10个方块中的表现为:只有0方块为好方块,其余9个方块都为坏方块如图:
_720w.jpg)
此时我们就可以计算出:
$TPR_1=1/7$
$FPR_1=0$
可以绘制ROC曲线上的一个点:

**设置第二个阈值**
同样,当我们设置阈值为0.85时,情况如下
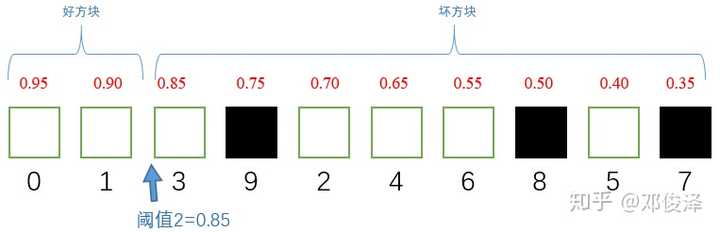
此时的TPR 与FPR分别为:
$TPR_2=2/7$
$FPR_2=0$
绘出ROC曲线上的第二个点:

设置11个阈值并且绘制ROC曲线
依次类推,我们设置11个阈值,阈值对应的FPR与TPR的点如下表:

对应的ROC图像中的点为

我们把每个点依次连起来,就能得到ROC曲线

ROC曲线的形状会同时受到**样本量**和各个**样本得分**的影响。可以认为阈值的选取是**任意值,无穷多**,所以ROC曲线的形状不受阈值选取的影响。我们平时看到的ROC曲线的样子就长下面这样:

##### 排序损失rank-loss
$l_{rank}=\frac{1}{m^+m^-}\sum_{x^+\in D^+}\sum_{x^-\in D^-}(\prod(f(x^+)给12张图片判断是不是5
下面是使用二分类器后训练出来的结果

| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| ------------ | ------------------------ | ------------------------ | ------------------------ | ------------------------ | ------------------------- | ------------------------- | ------------------------- | -------------------------- | -------------------------- | ------------------------- | ------------------------- | ------------------------- |
| 对应上面的图 | 8 | 7 | 3 | 9 | 5 | 2 | 5 | 5 | 6 | 5 | 5 | 5 |
m表示的是个数
D表示集合
m+表示是5的图片的个数
D+表示是5的集合
m-表示不是5的图片的个数
D-表示不是5的图片的集合
| | D | m |
| ---- | ------------------------------------------------------------ | ---- |
| + | D+={第5张图,第7张图,第8张图,第10张图,第11张图,第12张图,} | m+=6 |
| - | D-={第1张图,第2张图,第3张图,第4张图,第6张图,第9张图,} | m- |
然后给所有图打分
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| ------------------------------------------------------------ | ------------------------ | ------------------------ | ------------------------ | ------------------------ | ------------------------- | ------------------------- | ------------------------- | -------------------------- | -------------------------- | ------------------------- | ------------------------- | ------------------------- |
| 对应上面的图 | 8 | 7 | 3 | 9 | 5 | 2 | 5 | 5 | 6 | 5 | 5 | 5 |
| score,得分越高越有可能是5,
大于0的表示为机器识别为5,小于等于0的机器识别为不是5 | -1.2 | -1 | -0.8 | -0.7 | -0.4 | 0 | 0.2 | 0.4 | 0.5 | 0.7 | 0.9 | 1.3 |
| $f(x^-)$在D-中的位置大小 | -1 | -2 | -3 | -4 | | -5 | | | -6 | | | |
| $f(x^+)$在D+中的位置 | | | | | 1 | | 2 | 3 | | 4 | 5 | 6 |
这里的0代表一个阈值,因为是二分类,从0一分为二,负数不通过,正数通过。
可以提高,也可以下降,当阈值越低的时候,通过的数据就会越高,
比如,人脸识别一般超过80% 就通过,但是我们我们可以设置更加低的阈值50%,意味着更多的人通过人脸识别
这个题目的rank-loss
$\frac{1}{m^+m^-}=\frac{1}{6*6}$
$f(x^+) 对于一个模型,根据p不同,找到使得代价总期望最小的模型的阈值
横轴 $P(+)cost=\frac{p\times cost_{01}}{p\times cost_{01}+(1-p)\times cost_{10}},P(+)\in [0,1]$
纵轴为 $cost_{norm}=\frac{FNR\times p\times cost_{01}+FPR\times (1-p)\times cost_{10}}{p\times cost_{01}+(1-p)\times cost_{10}}$
$P(+)叫做正例概率代价$
$cost_{norm}叫做归一化代价,(也可以叫做总概率代价期望,错误率,犯错所需要付出的代价)$
$小p为现有的样本中正例出现的概率,对于上面判断是不是5的例子,小p=0.5,因为样本中12张图片,是5的一共有6张,所以为0.5$
意思为
$x=p(+)cost,$
$y=cost_{norm} $
$把x带入y中,变成关于x的函数为cost_{norm}=FNR\times P(+)+FPR\times P(+),$
$写成x和y的话,y=ax+b(1-x)\rightarrow y=(a-b)x+b,x\in [0,1],所以是一条直线$
问题一为什么会有这么多的直线呢????
因为一个阈值,之前的阈值是0,但是我们可以改变阈值,
一个阈值对应一个(FNR,FPR),一个(FNR,FPR)对应一条直线
改变阈值时,就会生成一条直线

问题二单根线段与横轴之间的(梯形)面积 = 模型对于某一阈值的期望总体代价?
**总体错误率”更为妥帖,即模型对于某一阈值的期望总体错误率**
所有线段围成的下包络线与横轴之间的面积 = 模型对于所有阈值的期望总体代价?
总体错误率,即模型对于某一阈值的期望总体错误率
## 1.9 比较检验