## 硬件平台说明 本项目硬件平台为RoboMaster C型开发板,Toolchain包含MDK5与Makefile,可使用Ozone进行调试(std.jdebug)。 ## 基于四元数扩展卡尔曼滤波的姿态更新算法 本算法利用四元数描述载体姿态,通过扩展卡尔曼滤波(Extended Kalman Filter, EKF)融合IMU数据,即利用加速度计修正姿态并估计陀螺仪 $x,y$ 轴零偏。并借助卡方检验剔除运动加速度过大时的加速度计量测以降低运动加速度对滤波准确性的影响。最终在STM32F4中利用C语言实现。采用记忆渐消因子避免零偏估计方差过度收敛。 ### 四元数 四元数定义: $$ \mathbf q=q_{0}^{}+q_{1}^{} i+q_{2}^{} j+q_{3}^{} k \quad(q_{0}^{}, q_{1}^{}, q_{2}^{}, q_{3}^{} \in \mathbb{R}) $$ 向量形式表示: $$ \mathbf q=\left[\begin{array}{l} {q_{0}^{}} \\ {q_{1}^{}} \\ {q_{2}^{}} \\ {q_{3}^{}} \end{array}\right] $$ 坐标变换矩阵$\boldsymbol C_b^n$: $$ \boldsymbol C_{b}^{n}=\left[\begin{array}{lll} {1-2\left(q_{2}^{2}+q_{3}^{2}\right)} & {2\left(q_{1} q_{2}-q_{0} q_{3}\right)} & {2\left(q_{1} q_{3}+q_{0} q_{2}\right)} \\ {2\left(q_{1} q_{2}+q_{0} q_{3}\right)} & {1-2\left(q_{1}^{2}+q_{3}^{2}\right)} & {2\left(q_{2} q_{3}-q_{0} q_{1}\right)} \\ {2\left(q_{1} q_{3}-q_{0} q_{2}\right)} & {2\left(q_{2} q_{3}+q_{0} q_{1}\right)} & {1-2\left(q_{1}^{2}+q_{2}^{2}\right)} \end{array}\right] $$ 四元数关于时间的微分方程为: $$ \dot{ \mathbf q} = \frac{1}{2}\boldsymbol \Omega\mathbf q $$ 其中: $$ \boldsymbol \Omega=\left[\begin{array}{cccc} {0} & {-\omega_{x}} & {-\omega_{y}} & {-\omega_{z}} \\ {\omega_{x}} & {0} & {\omega_{z}} & {-\omega_{y}} \\ {\omega_{y}} & {-\omega_{z}} & {0} & {\omega_{x}} \\ {\omega_{z}} & {\omega_{y}} & {-\omega_{x}} & {0} \end{array}\right] $$ 其中 $\omega_x,\omega_y,\omega_z$ 为 $b$ 系相对 $n$ 系的角速度。 ### 状态向量 定义状态向量为: $$ \boldsymbol x = \left[\begin{array}{c} \mathbf q \\ \boldsymbol \omega^{bias} \end{array}\right] $$ 其中 $\mathbf q = [q_0,q_1,q_2,q_3]^T$ 为机体坐标系 ($b$ 系) 相对惯性坐标系 ($n$ 系) 的姿态四元数。考虑一般姿态下 $b$ 系 $z$ 轴通常指天,故难以通过重力加速度估计其零偏,故定义 $\boldsymbol \omega^{bias} =[\omega^{bias}_x,\omega^{bias}_y]^T$ 为陀螺仪 $x,y$ 轴零飘。 ### 过程模型 根据陀螺仪误差模型,存在: $$ \boldsymbol \omega^{real} = \boldsymbol \omega^{measure} - \boldsymbol \omega^{bias} $$ 则过程模型为: $$ \begin{aligned} \boldsymbol x_{k+1} &= f(\boldsymbol x_k) + \boldsymbol {w}_{k} \\ &= \left[\begin{array}{c} \mathbf q_k +\frac{1}{2}\left(\boldsymbol \Omega_k - \boldsymbol \Omega_k^{bias} \right)\Delta t \mathbf q_k \\ \boldsymbol \omega^{bias} _k \end{array}\right] + \boldsymbol {w}_{k} \end{aligned} $$ 其中白噪声 $\boldsymbol {w}_{k} \sim N\left(\boldsymbol 0_{6 \times 1}, \boldsymbol {Q}\right)$,$\boldsymbol \Omega_k^{bias}$ 为陀螺仪零飘组成的矩阵。对非线性函数 $f$ 求其雅可比矩阵得 $\boldsymbol F_k$: $$ \begin{aligned} \boldsymbol F_k &=\frac{\partial f({\boldsymbol {x}}_{k})}{\partial {\boldsymbol {x}}_{k}}\\ &=\left[\begin{array}{cc} \boldsymbol I_{4} + {\frac{1}{2}\left(\boldsymbol \Omega_k - \boldsymbol \Omega_k^{bias} \right) \Delta t} & {\boldsymbol O_k} \\ {\boldsymbol 0_{2\times4}} & {\boldsymbol I_2} \end{array}\right] \end{aligned} $$ 其中矩阵 $\boldsymbol O_k$ 为: $$ \boldsymbol O_k = \begin{array}{c} \left[\begin{array}{cc} \frac{q_{1|k} \Delta t }{2} & \frac{q_{2|k}\Delta t }{2} \\ -\frac{q_{0|k} \Delta t}{2} & \frac{q_{3|k}\Delta t }{2} \\ -\frac{q_{3|k} \Delta t}{2} & -\frac{q_{0|k}\Delta t }{2} \\ \frac{q_{2|k} \Delta t}{2} & -\frac{q_{1|k}\Delta t }{2} \end{array}\right] \end{array} $$ ### 量测模型 根据 $\boldsymbol g=\boldsymbol C_{n}^{b}\left[\begin{array}{ccc}0&0&1\end{array}\right]^T$,在无运动加速度情况下有: $$ \begin{equation} \left[\begin{array}{lll} {2\left(q_{1} q_{3}-q_{0} q_{2}\right)} \\ {2\left(q_{2} q_{3}+q_{0} q_{1}\right)} \\ {1-2\left(q_{1}^{2}+q_{2}^{2}\right)} \end{array}\right]= \left[\begin{array}{c} a_x \\ a_y \\ a_z \end{array}\right] \end{equation} $$ 其中 $[a_x\ a_y\ a_z]^T$ 为归一化后向量,量测模型为: $$ \begin{equation} \boldsymbol z_{k} = h(\boldsymbol x_k) + \boldsymbol {v}_{k},\quad \boldsymbol {v}_{k} \sim N\left(\boldsymbol 0_{3 \times 1}, \boldsymbol {R}_k\right) \end{equation} $$ 其中非线性函数 $h(\boldsymbol x_k)$ 为: $$ h({\boldsymbol {x}}_{k}) =\left[\begin{array}{lll} {2\left(q_{1|k} q_{3|k}-q_{0|k} q_{2|k}\right)} \\ {2\left(q_{2|k} q_{3|k}+q_{0|k} q_{1|k}\right)} \\ {1-2\left(q_{1|k}^{2}+q_{2|k}^{2}\right)} \end{array}\right] $$ 根据四元数单位性质 $q_0^2+q_1^2+q_2^2+q_3^2=1$ 有: $$ \begin{equation} \begin{aligned} {\boldsymbol {H}}_k & = \frac{\partial h({\boldsymbol {x}}_{k})}{\partial {\boldsymbol {x}}_{k}} \\ & =\left[\begin{array}{ccccc} {-2q_{2|k}} & {2q_{3|k}} & {-2q_{0|k}} & {2q_{1|k}} & \boldsymbol 0_{1\times2} \\ {2q_{1|k}} & {2q_{0|k}} & {2q_{3|k}} & {2q_{2|k}} & \boldsymbol 0_{1\times2} \\ {2q_{0|k}} & {-2q_{1|k}} & {-2q_{2|k}} & {2q_{3|k}} & \boldsymbol 0_{1\times2} \end{array}\right] \end{aligned} \end{equation} $$ 另外,重力加速度向量垂直于惯性系,不能用于修正航向角,即状态 $q_3$ 不可观。为避免修正过程破坏航向角准确性,量测更新中修正值 $\boldsymbol K_k(\boldsymbol z_k - h(\hat{\boldsymbol {x}}^-_{k}))$ 不能用于修正状态变量 $q_3$,故定义修正量为: $$ \begin{equation} \boldsymbol M\boldsymbol K_k(\boldsymbol z_k - h(\hat{\boldsymbol {x}}^-_{k})) \end{equation} $$ 其中矩阵 $\boldsymbol M$ 为: $$ \boldsymbol M = \left[\begin{array}{cccccc} 1&0&0&0&0&0\\ 0&1&0&0&0&0\\ 0&0&1&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}\right] $$ 另外,为避免状态 $q_3$ 估计方差严重发散,矩阵 $\boldsymbol M$ 作用于修正量而非作用于卡尔曼增益 $\boldsymbol K_k$。 ### 卡方检验 量测模型的无偏性仅在不存在运动加速度的情况下成立,运动加速度的存在会导致量测更新出现误差。现实中机器人无运动加速度的稳态情况极少出现,为减小跳跃、撞击等情况下过大的运动加速度影响估计精度甚至稳定性,本算法通过卡方检验对加速度计量测信息进行检验。 定义残差: $$ \begin{equation} \boldsymbol e_k =\boldsymbol z_k-h(\boldsymbol {x}_{k}^-) \end{equation} $$ 正常情况下,残差 $\boldsymbol e_k$ 符合期望为 $\boldsymbol 0$ 的正态分布,其方差为: $$ \begin{equation} \boldsymbol D_k = E[\boldsymbol e_k\boldsymbol e_k^T]=\boldsymbol H_k\boldsymbol P_{k}^-\boldsymbol H_k^T + \boldsymbol R_k \end{equation} $$ 当突然产生较大运动加速度时,残差的值会显著大于一般情况,定义检测函数: $$ \begin{equation} r_k = \boldsymbol e_k^T\boldsymbol D_k^{-1}\boldsymbol e_k \end{equation} $$ 若 $r_k$ 大于阈值,本次量测存在较大运动加速度,则跳过本次量测更新仅进行预测更新。 #### 滤波器发散保护 若工作环境过于恶劣或卡方检验阈值设置过低会导致滤波器长时间不进行量测更新,进而导致协方差矩阵过大导致载体静止状态下残差仍无法通过卡方检验,这种情况需强制进行量测更新。 针对上述问题,本算法通过加速度与角速度测量值大小判断机体是否处于静止状态,若机体处于静止状态且无法通过卡方检验超过50次则设置ConvergeFlag为0,意味滤波器发散,要求暂时跳过卡方检验强制进行量测更新,直到检测函数值小于一定阈值时ConvergeFlag置1,意味滤波器收敛。 #### 增益自适应 若检查函数值较大,但仍能通过卡方检验,可根据检测函数值与卡方检验阈值的大小关系确定一个小于1的比例,作用于卡尔曼增益,以实现估计器增益的自适应。 #### 零偏修正限幅 为避免特殊情况下零偏估计协方差过大导致量测更新中零篇修正值过大产生突变,本算法对量测更新中零偏修正值进行限幅。 ### 渐消因子 考虑到陀螺仪零偏过程模型不完全精确,为避免随时间推移陀螺仪零偏估计协方差过度收敛,导致估计器对陀螺仪零偏无法适应由温度等因素引起的缓慢变化,进而无法得到无偏估计。为解决上述问题,可通过设置估计协方差矩阵对角线元素下限避免过度收敛,或通过渐消因子对协方差阵进行调整。 本算法采用渐消因子避免协方差矩阵过度收敛,定义渐消因子 $\lambda $ 为常数。考虑到仅需对陀螺仪零偏估计进行记忆渐消,故渐消因子 $\lambda $ 并不作用于整个协方差矩阵,定义矩阵 $\boldsymbol \Lambda$: $$ \boldsymbol \Lambda = \left[\begin{array}{cccccc} 1&0&0&0&0&0\\ 0&1&0&0&0&0\\ 0&0&1&0&0&0\\ 0&0&0&1&0&0\\ 0&0&0&0&\frac{1}{\lambda}&0\\ 0&0&0&0&0&\frac{1}{\lambda} \end{array}\right] $$ 于先验估计协方差更新前作用于协方差矩阵: $$ \boldsymbol P^*_{k+1}=\boldsymbol \Lambda\boldsymbol P_{k} $$ ### 算法更新流程 算法更新流程如下图所示:
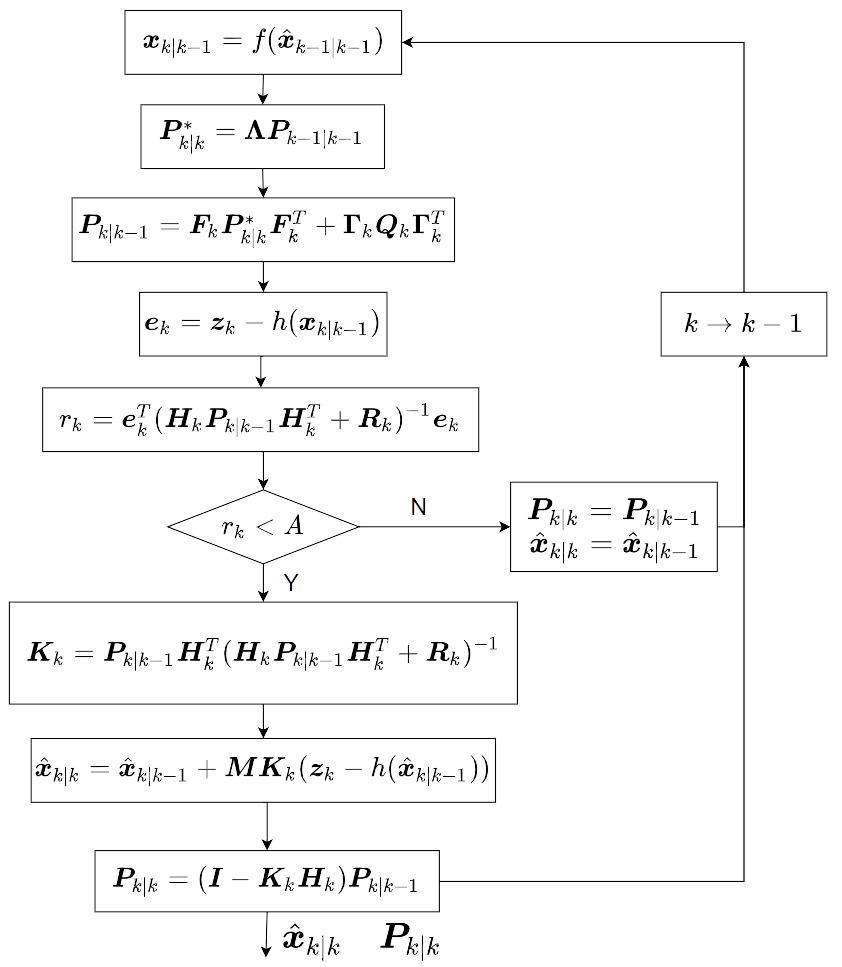 ### 试验验证
#### 零偏估计
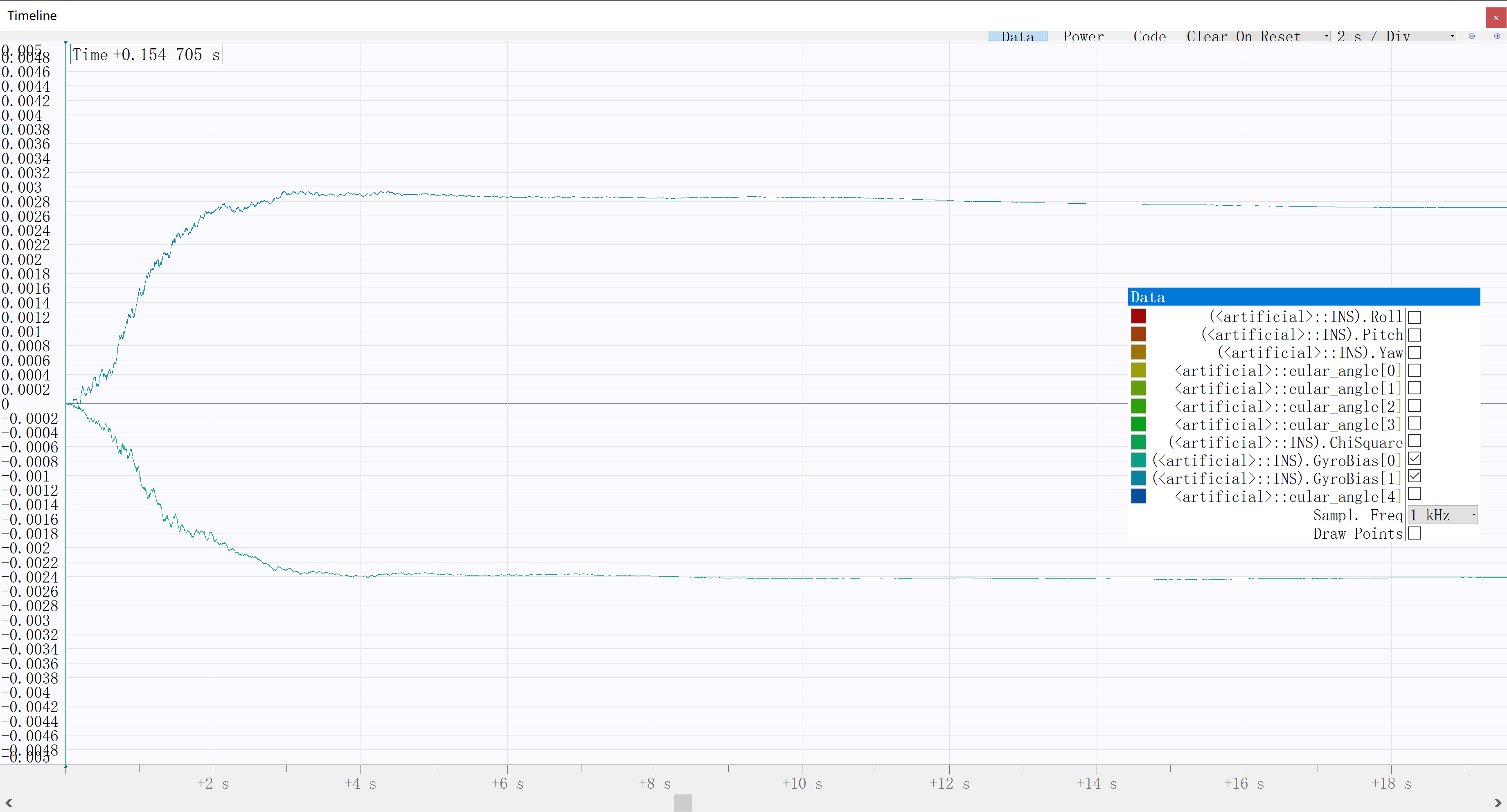
静止状态下开机 $x,y$ 轴零偏估计结果收敛情况如图所示:
### 试验验证
#### 零偏估计
静止状态下开机 $x,y$ 轴零偏估计结果收敛情况如图所示:
 静止状态下对比无额外零偏补偿的Mahony算法对俯仰角与横滚角的估计情况如图所示:
静止状态下对比无额外零偏补偿的Mahony算法对俯仰角与横滚角的估计情况如图所示:
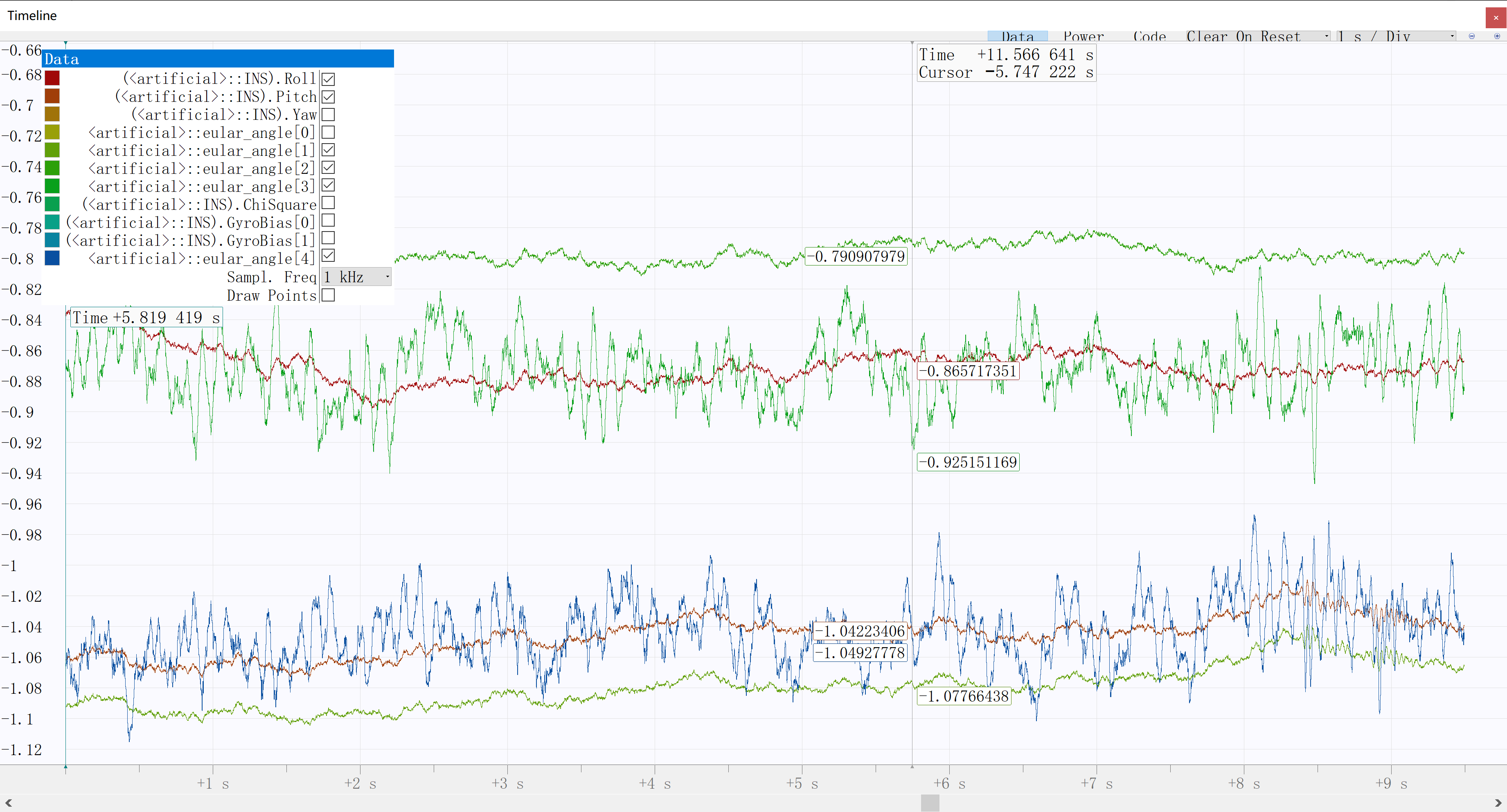 其中两条红色曲线为本文算法估计结果,两条噪声较小绿色曲线为无额外零偏补偿的Mahony算法估计结果,蓝色与噪声较大绿色的绿色曲线为加速度计正交分解得到的俯仰角与横滚角。
综上,陀螺仪零偏会使无零偏补偿的Mahony算法估计结果产生偏差,本文算法在静止状态下开机后可有效估计 $x,y$ 轴零偏并得到俯仰角与横滚角的无偏估计结果。
#### 运动加速度影响抑制
由于笔者没有姿态参考设备,故通过手持IMU并频繁甩动的方式施加运动加速度,甩动一段时间后使IMU保持静止,观察甩动结束后姿态角收敛情况,若静止后姿态角缓慢变化并最终收敛至与静止瞬间不同的结果,那么收敛值与静止瞬间值的差可以一定程度反应静止前姿态估计误差。
本文算法对比Mahony算法对俯仰角与横滚角的估计情况如图所示:
其中两条红色曲线为本文算法估计结果,两条噪声较小绿色曲线为无额外零偏补偿的Mahony算法估计结果,蓝色与噪声较大绿色的绿色曲线为加速度计正交分解得到的俯仰角与横滚角。
综上,陀螺仪零偏会使无零偏补偿的Mahony算法估计结果产生偏差,本文算法在静止状态下开机后可有效估计 $x,y$ 轴零偏并得到俯仰角与横滚角的无偏估计结果。
#### 运动加速度影响抑制
由于笔者没有姿态参考设备,故通过手持IMU并频繁甩动的方式施加运动加速度,甩动一段时间后使IMU保持静止,观察甩动结束后姿态角收敛情况,若静止后姿态角缓慢变化并最终收敛至与静止瞬间不同的结果,那么收敛值与静止瞬间值的差可以一定程度反应静止前姿态估计误差。
本文算法对比Mahony算法对俯仰角与横滚角的估计情况如图所示:
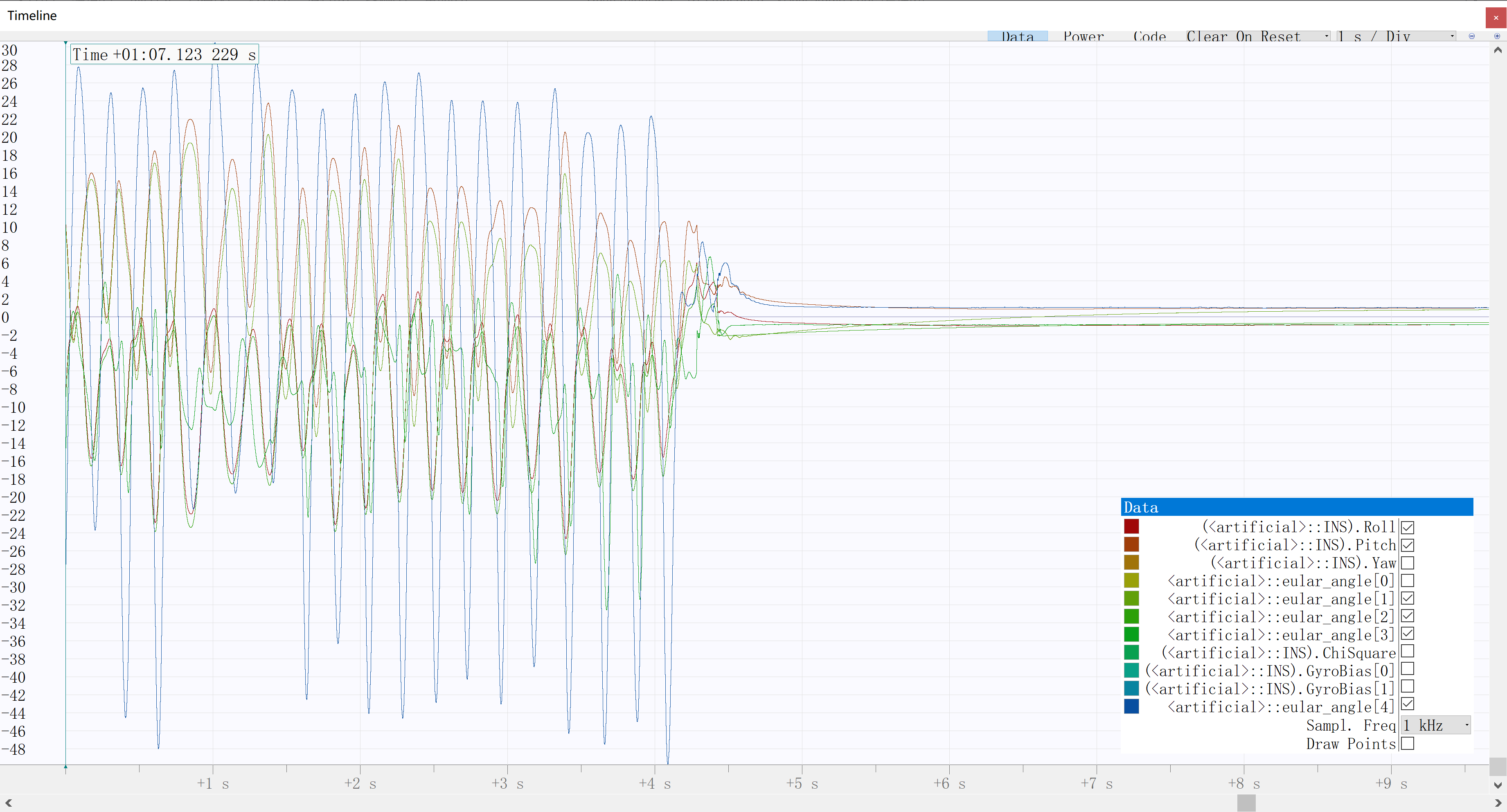 局部放大如图所示:
局部放大如图所示:
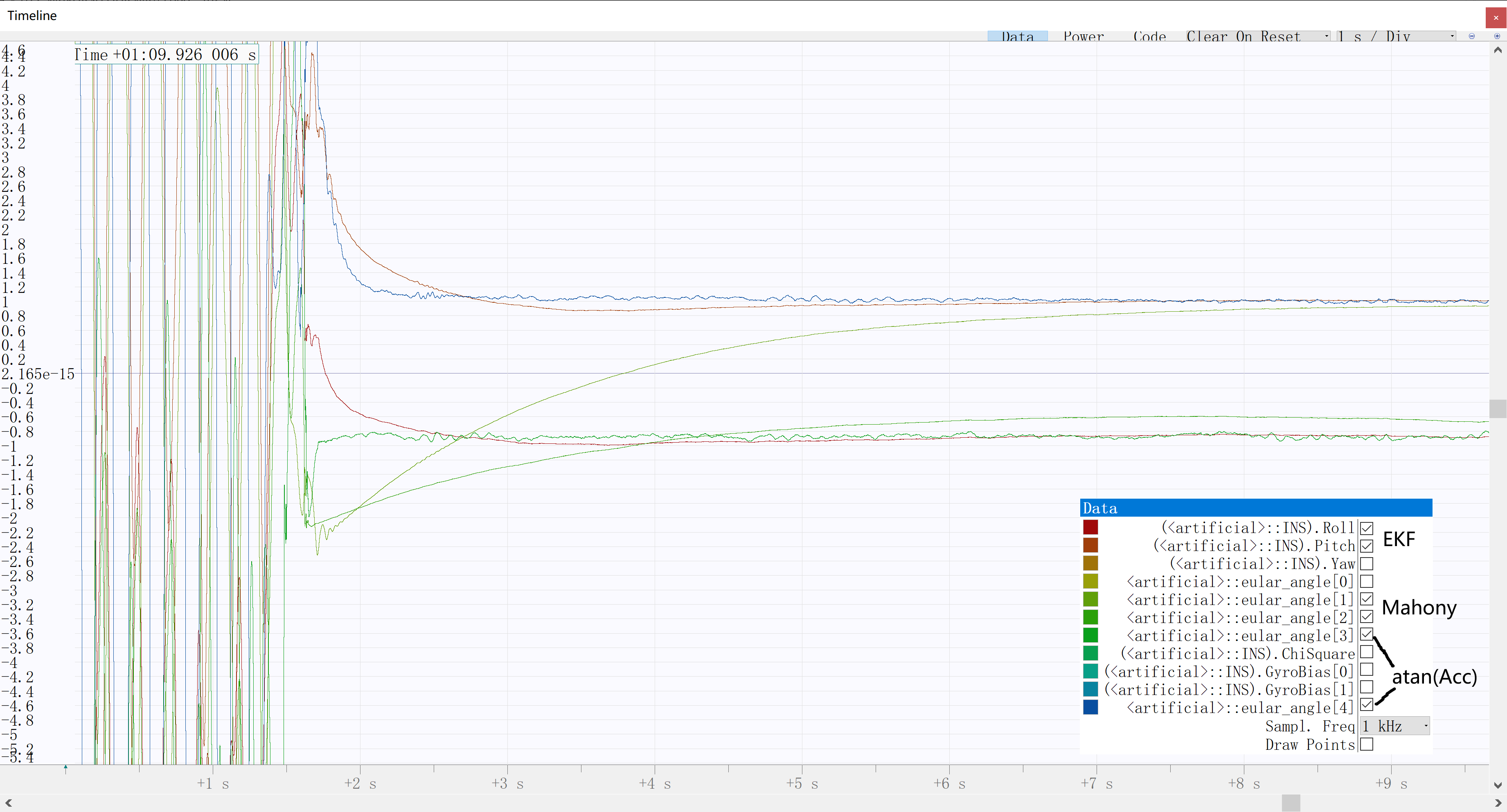 其中两条红色曲线为本文算法估计结果,两条噪声较小绿色曲线为无额外零偏补偿的Mahony算法估计结果,蓝色与噪声较大绿色的绿色曲线为加速度计正交分解得到的俯仰角与横滚角(经过一定低通滤波)。
综上,得益于卡方检验,本算法对运动加速度对姿态估计的不良影响具有一定程度的抑制作用。
其中两条红色曲线为本文算法估计结果,两条噪声较小绿色曲线为无额外零偏补偿的Mahony算法估计结果,蓝色与噪声较大绿色的绿色曲线为加速度计正交分解得到的俯仰角与横滚角(经过一定低通滤波)。
综上,得益于卡方检验,本算法对运动加速度对姿态估计的不良影响具有一定程度的抑制作用。