# Extended-Kalman-Filter-Project
**Repository Path**: wpc94/Extended-Kalman-Filter-Project
## Basic Information
- **Project Name**: Extended-Kalman-Filter-Project
- **Description**: No description available
- **Primary Language**: C++
- **License**: Not specified
- **Default Branch**: master
- **Homepage**: None
- **GVP Project**: No
## Statistics
- **Stars**: 0
- **Forks**: 1
- **Created**: 2024-08-12
- **Last Updated**: 2024-08-12
## Categories & Tags
**Categories**: Uncategorized
**Tags**: None
## README
# Extended Kalman Filter Project Starter Code
This project involves the Simulator which can be downloaded [here](https://github.com/udacity/self-driving-car-sim/releases).
This repository includes two files that can be used to set up and install [uWebSocketIO](https://github.com/uWebSockets/uWebSockets) for either Linux or Mac systems. For windows you can use either Docker, VMware, or even [Windows 10 Bash on Ubuntu](https://www.howtogeek.com/249966/how-to-install-and-use-the-linux-bash-shell-on-windows-10/) to install uWebSocketIO. Please see the uWebSocketIO Starter Guide page in the classroom within the EKF Project lesson for the required version and installation scripts.
Once the install for uWebSocketIO is complete, the main program can be built and run by doing the following from the project top directory.
1. mkdir build
2. cd build
3. cmake ..
4. make
5. ./ExtendedKF
Tips for setting up your environment can be found in the classroom lesson for this project.
Note that the programs that need to be written to accomplish the project are src/FusionEKF.cpp, src/FusionEKF.h, kalman_filter.cpp, kalman_filter.h, tools.cpp, and tools.h
The program main.cpp has already been filled out, but feel free to modify it.
Here is the main protocol that main.cpp uses for uWebSocketIO in communicating with the simulator.
**INPUT**: values provided by the simulator to the c++ program
["sensor_measurement"] => the measurement that the simulator observed (either lidar or radar)
---
## Other Important Dependencies
* cmake >= 3.5
* All OSes: [click here for installation instructions](https://cmake.org/install/)
* make >= 4.1 (Linux, Mac), 3.81 (Windows)
* Linux: make is installed by default on most Linux distros
* Mac: [install Xcode command line tools to get make](https://developer.apple.com/xcode/features/)
* Windows: [Click here for installation instructions](http://gnuwin32.sourceforge.net/packages/make.htm)
* gcc/g++ >= 5.4
* Linux: gcc / g++ is installed by default on most Linux distros
* Mac: same deal as make - [install Xcode command line tools](https://developer.apple.com/xcode/features/)
* Windows: recommend using [MinGW](http://www.mingw.org/)
## Basic Build Instructions
1. Clone this repo.
2. Make a build directory: `mkdir build && cd build`
3. Compile: `cmake .. && make`
* On windows, you may need to run: `cmake .. -G "Unix Makefiles" && make`
4. Run it: `./ExtendedKF `
# Extended Kalman Filter
> 卡尔曼滤波(Kalman
> filtering)是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
## 自动驾驶中的卡尔曼滤波
例如使用卡尔曼滤波器来预测前方的车辆将采取的下一组动作,预测汽车周围的其他汽车或者自行车的位置。是一个迭代的过程,通过对于前一个状态的预测值,加上实际的测试值,来预测下一个状态的状态值。
在这里边的先验值,测量值,预测值均符合正态分布。使用两个正态分布的相关量可以预测出第三个相关量,也是符合正态分布。
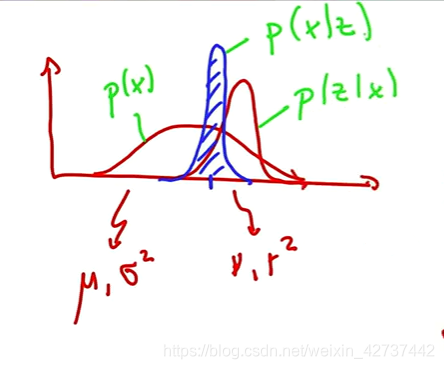

使用一个状态的值预测下一个状态的值
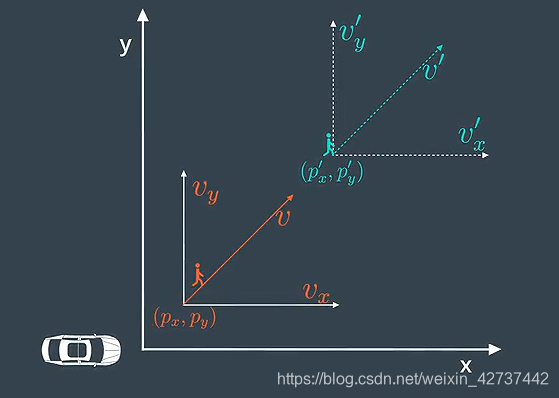
## 卡尔曼滤波器的原理
卡尔曼滤波器是一个迭代的过程,主要是两个阶段,第一个阶段是预测,第二个阶段是更新。
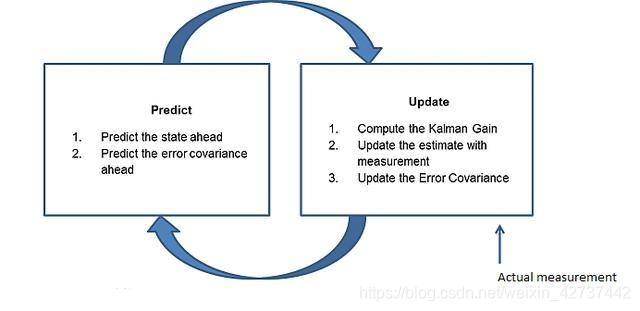
### 预测
在该步骤中,卡尔曼滤波器根据初始值预测新值,然后根据系统中存在的各种过程噪声引入预测中的不确定性。
可以使用一个简单的例子来理解噪声,假设我们的汽车在判断前边的一辆自行车的运动轨迹,如果不计算自行车的加速度,那么自行车就是以恒定速度移动,但实际上它将具有加速度,即速度将不时波动。这种加速度的变化就是不确定性,我们使用过程噪声将其引入我们的系统。
### 更新
在此步骤中,我们从系统的设备中获取实际测量值。在自动驾驶车辆的情况下,这些设备可以是雷达或激光雷达。然后我们计算预测值和测量值之间的差值,然后通过计算卡尔曼增益来决定预测值或测量值的权重。根据卡尔曼增益做出的决定,我们计算新值和新的不确定性。
### 卡尔曼滤波的公式
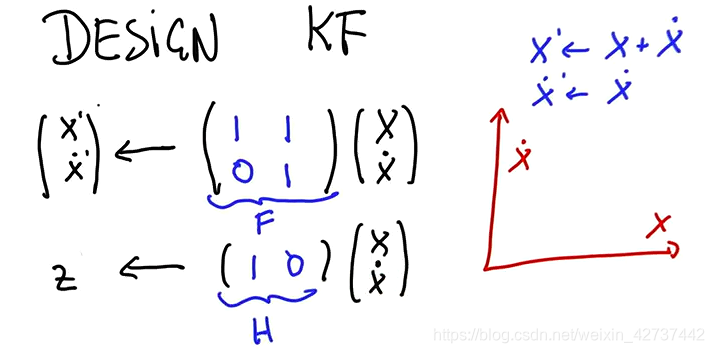

F--状态转移矩阵
H--状态变量到测量(观测)的转换矩阵,表示将状态和观测连接起来的关系,卡尔曼滤波里为线性关系,它负责将 m 维的测量值转换到 n 维,使之符合状态变量的数学形式,是滤波的前提条件之一。
P--描述不确定性的协方差矩阵
u--运动向量
Z--测量值
R--测量噪声
I--单位矩阵
## 传感器融合
雷达可以探测到物体的速度信(矢量),激光雷达可以探测到物体的位置信息,即距离,因此我们想要将两种传感器融合,来准确的探测物体,从而预测物体的位置。
我们想要将两种数据融合起来,一起放入卡尔曼滤波器中。
### 卡尔曼滤波器的流程;

- **first measurement** 滤波器在第一次运行的时候接受雷达和激光雷达的数据初始化自行车起始位置。
- **initialize state and covariance matrices** 该过滤器将基于所述第一次测量初始化自行车的位置。
- 然后,该车将一个时间段Δt之后接收另一组传感器数据。
- **predict** 该算法将预测时间Δt之后该自行车的位置。一种预测的方案是假设自行车在Δt内是匀速行驶的,所以自行车的速度V是一个常数,因此我们认为自行车走过的距离为V*Δt。在扩展卡尔曼滤波器中,我们认为速度是恒定的,但是在无迹卡尔曼滤波器中,我们会定义更加复杂的模型。
- **update** 滤波器将会比较自行车预测的位置和实际上测量到的位置,然后将两个数据综合起来,给出新的预测的位置。滤波器将会更具每个值的不确定度给予相应的权重。
- 然后再经过Δt的时间,传感器又会给出新的值,于是现在的预测值跟传感器的测量值结合,就又可以开始新一轮的预测。
卡尔曼滤波器工作流程:

- x是平均状态向量。对于一个扩展卡尔曼滤波器来说,平均状态向量包含了你在追踪的物体的位置信息和速度。之所以被命名为“平均”状态向量,是因为位置和速度可以表示为均值为x的高斯分布。
- p是状态协方差矩阵,它包含了物体位置和速度的不确定性信息。你可以理解为标准差。
- k是时间间隔。因此,xk表示物体在k时刻的位置和速度。
- k+1∣k表示预测步骤,在k+1时刻,可获得传感器的采集数据。考虑传感器数据是为了获知新的物体位置和速度信息,在此之前,你需要预测k+1时刻物体的位置和速度。你可以根据k时刻物体的位置和速度信息来预测其k+1时刻的位置。因此,xk+1∣k表示我们已经预测到k+1时刻物体的位置信息,但还没有用传感器进行测试。
- xk+1表示我们已经预测到k+1时刻物体的位置信息,以及考虑到传感器信息后更新的物体位置和速度信息。
- 如果雷达和激光雷达的传感器数据在k+3时刻同时到达,先预测xk+3,然后用任意一个传感器信息进行更新。得到新的新的xk+3之后,再使用另一个传感器信息进行更新。
### 实现

#### 预测
比方说,我们知道一个物体的当前位置和速度,我们将状态保存在x变量中,就是状态向量。假设这个物体的速度恒定,我们就可以推算出一秒钟之后的该物体的速度和位置,因为我们知道它前一刻的状态并且速度恒定。
X'= FX +ν这个方程就是我们做预测的一个计算过程。
但是我们知道很多的时候物体的运动速度并不是恒定的,有可能改变了运动方向,有可能进行了加速减速,所以预测之后,我们的预测到的位置时不确定的,有一个不确定性,所以我们用P'= FPF T + Q来表示这种增加的不确定性。
过程噪声指的是在预测步骤中的不确定性。我们假设物体移动以恒定的速度,但在现实中,对象可能加速或减速。符号ν~N(0,Q)定义的过程噪声均值为零,方差为Q的高斯分布。
#### 更新
在更新步骤,我们从传感器得到了物体相对于汽车的位置信息,首先我们利用传感器的数据计算出实际位置:
y=Z − Hx`
**矩阵K**一般被叫做卡尔曼增益,结合了我们预测的带有不确定性的位置P`和传感器的测量误差R,如果我们传感器测量的误差很大,那么卡尔曼滤波器就会给我们的预测值分配更大的权重,如果我们预测值的不确定性更高,那就给测量值分配更大的权重。
**测量噪声**是指在传感器测量的不确定性。符号ω~N(0,R)定义了测量噪声均值为零,方差为R的高斯分布.测量噪声来自于传感器测量值的不确定性。
#### 关于状态转换函数:Bu
实际上的状态转移方程是x′=Fx+Bu+ν,但是我们这里只留下了X'= FX +ν
B叫做控制输入矩阵,u是控制向量。
举个例子,假设我们在追踪一辆汽车,我们知道对于某个汽车的发动机的加减速特性,换句话说,我们有一个动力学模型。Bu将代表由于发动机的内部动力导致的汽车的位置的变化。我们会用ν表示任何随机噪声,我们一样无法准确预测,比如车子会在路上打滑或者会有强风给车一个不确定的加速度。
在此处,我们将假定没有办法来衡量或不知道被跟踪对象的确切加速度。例如,如果我们在追踪自行车,行人或另一辆汽车,我们不能知道其他对象的内部力模型;因此,我们不知道某些其他物体的加速度是什么。相反,我们将设置BU = 0,代表加速度均值ν随机噪声。
## 卡尔曼滤波器实现

### 预测
首先,X为状态向量,包含了位置和速度,既(Px,Py,vx,vy).
那么状态转移方程为x′=FX+noise: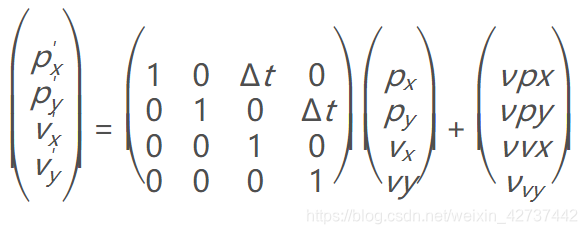
其次,要计算描述不确定性的协方差矩阵P:
在这里我们使用了σax2和σay2,这两个参数是加速噪声参数。
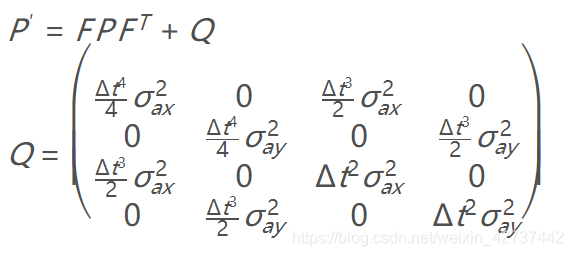
因为我们的状态向量只跟速度和位置有关系,所以我们要在建模中添加随机噪声,一般来说,两次更新间隔的时间越长,即Δt越大,那么不确定性也会越大。
结合位置和速度的关系,我们有以下的公式:
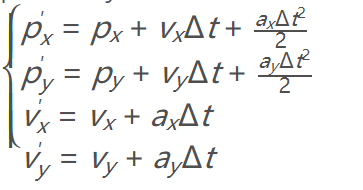
由于加速度是未知的,我们可以把它添加到噪声成分,而这种随机噪声会被解析表示为公式中的最后一个条件之上的。因此,我们的速度矢量中就有了加速度的噪声成分:
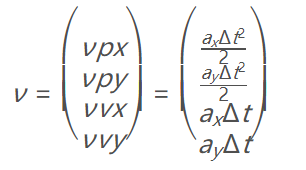
这是由一个零均值和协方差矩阵Q所描述的,所以ν~N(0,Q)。
v可以分解为一个4X2的不含加速度的矩阵和一个2X1的加速度矩阵相乘:
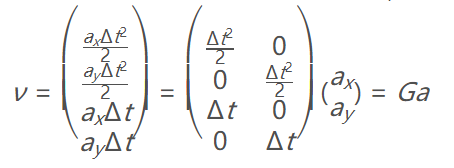
Δt是一个已知量 ,为时间间隔,加速度服从均值是0 ,标准差为σax<和σay。
基于我们的噪声向量现在我们可以定义新的协方差矩阵Q,可以表示为噪声向量v乘以噪声向量vT。
表示为以下的样子:
Q=E[ννT]=E[GaaTGT]
由于G不包含随机变量,所以可以简化为这样:

假设ax,ay是不相关的,所以有了以下简化:
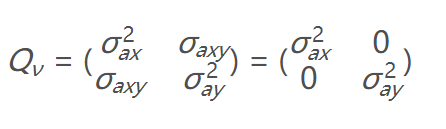
结合了所有的矩阵,综上以后,得到Q:
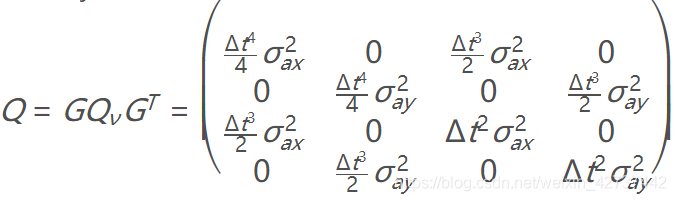
```cpp
float dt = (measurement_pack.timestamp_ - previous_timestamp_) / 1000000.0; //dt - expressed in seconds
previous_timestamp_ = measurement_pack.timestamp_;
float dt_2 = dt * dt;
float dt_3 = dt_2 * dt;
float dt_4 = dt_3 * dt;
//Modify the F matrix so that the time is integrated
ekf_.F_(0, 2) = dt;
ekf_.F_(1, 3) = dt;
//set the acceleration noise components
float noise_ax = 9;
float noise_ay = 9;
//set the process covariance matrix Q
ekf_.Q_ = MatrixXd(4, 4);
ekf_.Q_ << dt_4 / 4 * noise_ax, 0, dt_3 / 2 * noise_ax, 0,
0, dt_4 / 4 * noise_ay, 0, dt_3 / 2 * noise_ay,
dt_3 / 2 * noise_ax, 0, dt_2*noise_ax, 0,
0, dt_3 / 2 * noise_ay, 0, dt_2*noise_ay;
```
### 更新
#### H和h(x)
对于激光雷达和毫米波雷达,都在更新中需要用到H,但是H对于两种传感器略有不同。
##### 激光雷达
z是测量向量,y=z−Hx′,对于激光雷达,z包含了x,y坐标值。
H是一个将我们预测值转换到实际测量值空间的向量,也就是说,对于激光雷达,我们的测试值只包含x,y的位置信息,所以我们要舍弃速度信息,因此,有了以下的变化:
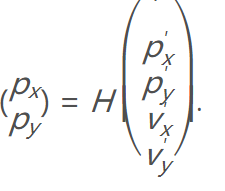

- 测量噪声协方差矩阵R
对于激光雷达来说,我们的测量值包含了x和y,并且每一个维度上都会有一个误差,
所以我们的噪声矩阵 ω 与Z有着相同的大小,R是测量噪声协方差矩阵,换句话说,矩阵R表示在我们从激光雷达上接收所述位置测量的不确定性:
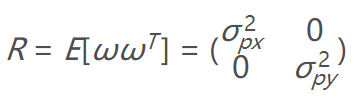
通常情况下,这些误差都由设备制造商给出,**对角线为0代表这些噪声是不相关的**
```cpp
void KalmanFilter::Update(const VectorXd &z) {
VectorXd y = z - H_ * x_;
MatrixXd S = H_ * P_ * H_.transpose() + R_;
MatrixXd K = P_ * H_.transpose() * S.inverse();
x_ = x_ + (K * y);
long x_size = x_.size();
MatrixXd I = MatrixXd::Identity(x_size,x_size);
P_ = (I - ( K * H_ )) * P_;
}
```
##### 激毫米波雷达
对于毫米波雷达来说,测量的参数是极坐标下的参数,需要我们手动将笛卡尔坐标系下的状态向量转化成极坐标下的( ρ,ϕ,ρ`),所以需要定义一个h(X)的矩阵来进行转换。
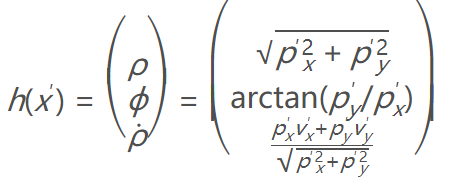
因此对于毫米波雷达来说,y=z−Hx′就变成 y=z−h(x′)。
具体推导过程

但是这会带来一个问题,当一组符合高斯分布的数据,经过一个额非线性变换之后,并不一定符合高斯分布,例如下图:
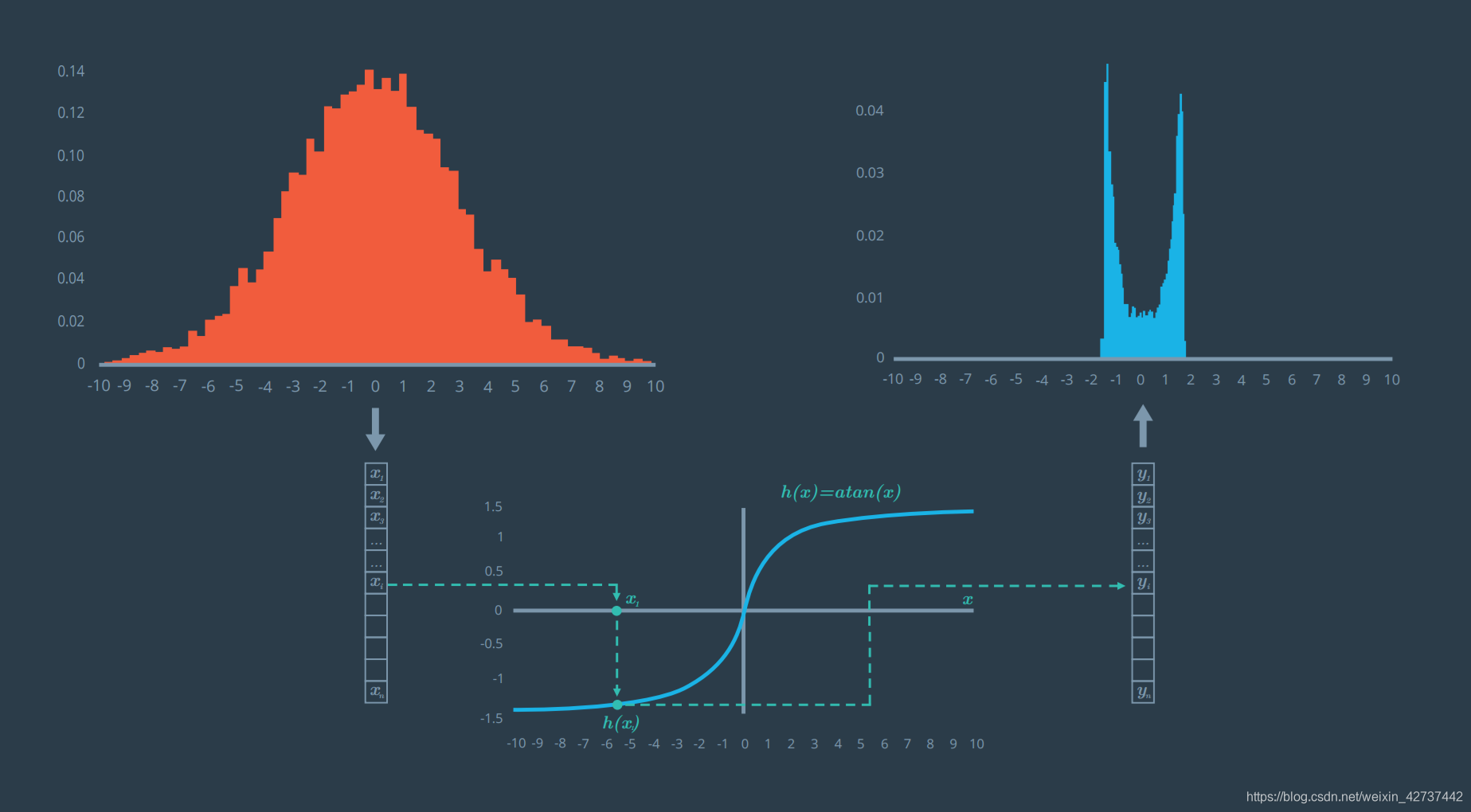
一组符合高斯分布的数据,经过atan的变换之后,就不符合高斯变换了,因此就不能使用卡尔曼滤波器的算法去更新(卡尔曼滤波器需要数据符合高斯分布),这可怎么办呢?就需要使用到扩展卡尔曼滤波算法,其核心思想就是使用一阶泰勒展开,说人话就是利用相应点的导数来构建线性方程,使用线性方程取代非线性方程的变换,从而使数据仍然符合正态分布。
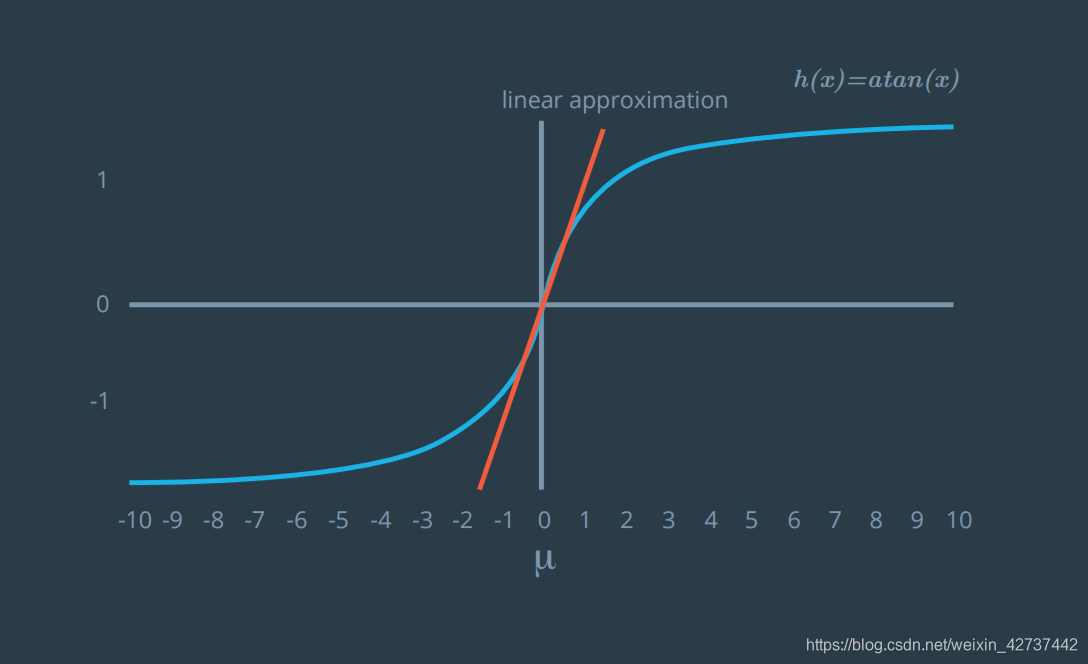
在这里我们就用到了**雅可比矩阵(Jacobian Matrix )**
> 在向量微积分中,雅可比矩阵是一阶偏导数以一定方式排列成的矩阵,其行列式称为雅可比行列式。雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。因此,雅可比矩阵类似于多元函数的导数。
所以我们要对h(X)计算雅可比矩阵。
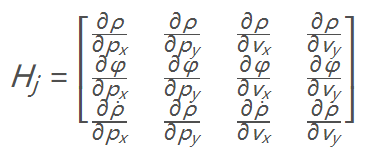

所以最后Hj为:
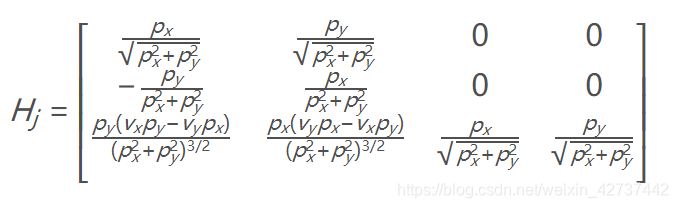
```cpp
MatrixXd Tools::CalculateJacobian(const VectorXd& x_state) {
MatrixXd Hj(3,4);
float px = x_state(0);
float py = x_state(1);
float vx = x_state(2);
float vy = x_state(3);
float c1 = px * px + py * py ;
float c2 = sqrt(c1);
Hj << px / c2 , py / c2 , 0 , 0 ,
-py / c1 , px / c1 , 0 , 0 ,
(py * ((vx * py) - (vy * px))) / (c1 * c2),(px *((vy * px) - (vx * py))) / (c1 * c2) , px/c2 ,py / c2;
return Hj;
}
```
计算出了y之后,就可以根据卡尔曼滤波器的公式依次带入,最后计算出每次的预测值。
```cpp
void KalmanFilter::UpdateEKF(const VectorXd &z) {
float ro = sqrt(x_(0) * x_(0) + x_(1) * x_(1));
float theta = atan2(x_(1), x_(0));
float ro_dot;
if(ro < 0.0001){
ro_dot = 0;
}else
{
ro_dot = (x_(0) * x_(2) + x_(1) * x_(3)) / ro;
}
VectorXd hx(3);
hx << ro,theta,ro_dot;
//此处的H_已在上层被赋值为为Hj
VectorXd y = z - hx;
MatrixXd S = H_ * P_ * H_.transpose() + R_;
MatrixXd K = P_ * H_.transpose() * S.inverse();
x_ = x_ + K * y;
long x_size = x_.size();
MatrixXd I = MatrixXd::Identity(x_size,x_size);
P_ = (I - ( K * H_ )) * P_;
}
```
**需要在每次更新前判断不同的传感器数据,来选择不同的卡尔曼滤波器:**
```cpp
if (measurement_pack.sensor_type_ == MeasurementPackage::RADAR) {
// Radar updates
Tools tools;
Hj_ = tools.CalculateJacobian(ekf_.x_);
ekf_.H_ = Hj_;
ekf_.R_ = R_radar_;
ekf_.UpdateEKF(measurement_pack.raw_measurements_);
} else {
// Laser updates
ekf_.H_ = H_laser_;
ekf_.R_ = R_laser_;
ekf_.Update(measurement_pack.raw_measurements_);
}
```
最后,还可以计算一下均方根误差:
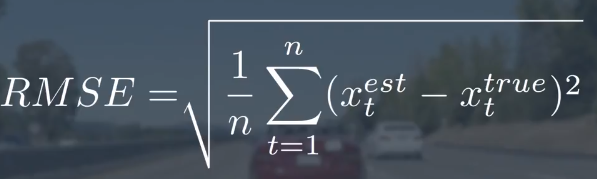
```cpp
VectorXd Tools::CalculateRMSE(const vector &estimations,
const vector &ground_truth) {
VectorXd RMSE(4);
if (estimations.size() != ground_truth.size() || estimations.size() == 0 ){
std::cout << "Invalid estimation or ground_truth data" << std::endl;
return RMSE;
}
// calculate sum
for(int i = 0;i < estimations.size();i++){
VectorXd residual = estimations[i] - ground_truth[i];
VectorXd residual_sq = residual.array() * residual.array();
RMSE += residual_sq;
}
//calculate mean
RMSE = RMSE / estimations.size();
//calculate square
RMSE = RMSE.array().square();
return RMSE;
}
```